Allium test - Статистическая обработка данных

Биология - Allium test - Статистическая обработка данных

14 мая 2011

Оглавление:
1. Allium test
2. История метода «Allium Test», преимущества перед другими методами и перспективы
3. Преимущества метода Allium cepa
4. Характеристика лука Allium cepa L., применимость в тестах
5. Методика проведения тестирования
6. Макроскопические исследования
7. Микроскопические исследования и статистическая обработка
8. Статистическая обработка данных

Статистические методы

Среднее арифметическое

Вариантным является каждый корешок. Если вариант меньше 30, следует пользоваться прямым способом: все варианты суммируются и полученная сумма делится на число вариант:

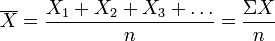
$\overline X = \frac {X_1 + X_2 + X_3 + \dots}{n} = \frac {\Sigma X}{n}$ , где ΣX — сумма вариант,
n — здесь и далее количество проанализированных вариантов.

Полученные интегральные данные о фазных индексах подвергают статистической обработке. Обработку проводят по формулам для малых выборок.

Среднее квадратическое отклонение σ

Для малых выборок σ рассчитывается по формуле:

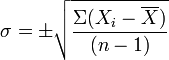
$\sigma=\pm \sqrt{\frac{\Sigma}{}}$

Среднее квадратичное отклонение характеризуется разнообразием признаков. Оно учитывает отклонение от среднеарифметической каждой варианты. Поэтому σ является наилучшим показателем разнообразия признака.

Средняя ошибка для оценки достоверности средней арифметической

Для малых выборок:

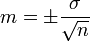
$m=\pm\frac{\sigma}{\sqrt n}$

, где m — ошибка среднего,
σ — среднее квадратичное отклонение

Средние арифметические, характеризующие действие изучаемого вещества на митотическую активность клеток меристемы Allium cepa, рассчитаны для небольшого числа повторностей. Достоверность для всей генеральной совокупности устанавливается при помощи средней ошибки.

Величина средней ошибки находится в обратной зависимости от n. Таким образом, чем больше повторностей опыта исследуется, тем меньше ошибка X.
Величину X следует записывать с величиной его ошибки:

Обозначение	Пример	Вид графика
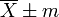$\overline X \pm m$	5 ± 0,5 %

Число степеней свободы

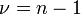
$\mathsf\nu=n-1$

Нахождение показателя достоверности разницы осуществляется в несколько этапов. Вычисляется число степеней свободы.

t-критерий Стьюдента

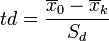
$td=\frac{\overline x_0 - \overline x_k}{S_d}$
, где X₀ — среднее арифметическое опытного варианта,
X_k — среднее арифметическое контрольного варианта,
S_d — ошибка отклонения, которая определяется при n₁ 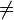$\not=$ n₂

Далее следует сравнить рассчитанные средние арифметические значения индекса контрольного и опытного вариантов. X двух сравниваемых групп, даже взятых из одной генеральной совокупности, всегда могут в какой-то мере отличаться друг от друга. Для чего выясняем, являются ли различия между средними арифметическими контрольного и опытных вариантов достоверными, или же это различие случайно. Для выяснения вопроса можно воспользоваться t-критерием Стьюдента.

Ошибка отклонения

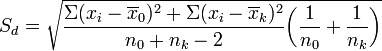
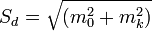
при n₁≠n₂ $S_d=\sqrt{\frac{\Sigma^2+\Sigma^2}{n_0+n_k-2}{\left}}$ , если n₁=n₂ $S_d=\sqrt{}$

Более подробно в методическом пособии.

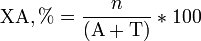
$\mbox{XA}, %=\frac{n}{}*100$

Программно-статистические методы

Проводиться с использованием математических пакетов. Для статистического анализа данных, полученных методом Allium test можно использовать само вычисляющую электронную таблицу, совместимую с MS Excel или LO Calc.

В таблице есть возможность эффективно группировать данные на листе, предоставляя выходные данные в удобном для последующей обработки и использования, виде, а так же в будущем наращивать функционал таблицы под специфические задачи или при расширении обсчитываемых параметров теста.

<<< Модельные организмы

Caenorhabditis elegans >>>

Адаптация
Биологи
Биологические законы
Биологические циклы
Биологическое оружие
Биоэтика

История биологии
Биологическая кибернетика
Книги по биологии
Латинские фразы и выражения в биологии и медицине
Методы биологических исследований
Биологические награды

Биологическое образование
Биологические организации
Организмы
Популяризация биологии
Биологические процессы
Симметрия (биология)